参考文献

[1] 热力学. 王竹溪, 北京大学出版社 2004

[2] Thermodynamics. Ryogo Kubo, North-Holland Publishing Company 1968

[3] Thermodynamics. Enrico Fermi, Dover Publications 1956

[4] Thermodynamics and Statistical Mechanics. Arnold Sommerfeld, Academic Press 1956

[5] 微分几何讲义. 周建伟, 科学出版社 2010

[6]

Acknowledgement

在写作本文的过程中，Jyx 检查了文章草稿并给出了宝贵的建议. 特别是文中关于 Clausius 不等式的连续形式的证明思路得益于与 Jyx 的讨论.

热力学杂谈

热力学第一定律

首先考虑热力学第一定律. 平衡态体系存在许多状态参量，其中最为重要的恐怕就是内能和熵. 然而，内能与熵之间亦有不同. 第一定律是说，在任意过程中，内能的变化总是可以归结为传热与做功之和：这就是说热与功都可以同样地改变物体的内能，并且两者的贡献相互独立.

这当然是一种能量守恒律的体现. 然而第一定律的内涵不止于此. 首先就是可以注意到，式子

的左边涉及到体系的内能，而式子的右边则涉及到过程量. 严格来说，外界对系统做功的量 无论对于平衡态还是非平衡态系统，都是可以测量的. 然而内能 是仅对平衡态体系(下文中会进行进一步讨论)定义的，因而式子 (1) 是定义了两个平衡态的内能之差与传热和做功的联系.

根据文献 [1] 的说法，热量 的确是后于内能而定义的：Joule 的能定理确立了内能这个态函数的存在性，而热量的定义则需要从热力学第一定律导出：

并且文献 [1] 的第 48 页也明确指出，"为说明内能，我们将假设物体处在平衡态". 不过其实严格来说，用两个平衡态之间的绝热过程的做功的量来定义这两个平衡态的内能之差，还是隐含了"任意两个平衡态都可以由绝热过程连接"这个假设. 虽然说如果考虑一般的不可逆的绝热过程，那么这个假设似乎应当成立，但是这也并不是不证自明的. 文献 [3] 的第 14 页提出，传热可以等价于一个借助于耗散媒介的做功过程:譬如说要使得水的温度上升，可以直接放在炉子上加热，也可以用叶片在水中搅动。说得更详细一些，可以设计一个隔热的容器，其中装有一些水，通过转动一个把手，可以通过一个连杆机构使得容器内的叶片发生相应的转动，这种转动通过叶片与水的摩擦转化为热量(严格来说还涉及水的各个部分之间的能量传递过程)，从而使得水的温度最终上升. 这里，叶片与连杆机构就使得外界的做功完全转化为热. 虽然这也仅仅是一个例子，但还是可以说明功转化为热是完全具有可实施性的(然而另一个方向上的热转化为功确会受到热力学第二定律的限制：不可能找到这样一种媒介(也即热机)，使得系统放出的热量最终转化为等量的功). 因此，假设系统从某个平衡态出发，经过某个涉及到吸热的过程，最终达到另一个平衡态，那么就可以通过中介的手段来将其中的传热过程替换为做功. 如果设涉及到放热，那么要确定这两个态的内能之差，就只需考虑其逆过程. 但是对于一般的同时涉及到吸热和放热的过程，上述办法就行不通了.

由此可见，还是直接将内能的存在作为一个经验事实加以接受较为稳妥，或者如文献 [2] pp.5 的处理，说将热量 预先当作是可以被准确测量的，之后再通过热力学第一定律引入内能.

虽然说第一定律 (1) 中假设体系的初末状态都是平衡态，但实际上内能的概念仍可作大幅度的延申. 这主要利用了以下事实：任何孤立体系在足够长的时间内都会趋于平衡态(文献 [1] pp.6, 文献 [2] pp.2). 这里的"孤立"的含义 是指系统与外界无任何相互作用，并且通常也假设系统被约束在有限的空间范围之内. 譬如说宇宙本身是一个无界系统，因而一般来说不能算作是这里所说的"孤立体系".

现在假设 为非平衡态，那么可以设想一个过程 在此过程中， 作为孤立系统演化到平衡态 那么由于此过程中体系与外界不发生热和功的交换，因此平衡态 的内能 必定与过程的具体细节无关. 因而实际上非平衡态 的内能是可以通过这种思想实验加以定义的：定义 即可.

然而，非平衡系统的熵的定义就远没有这么简单. 譬如说假设有一个隔热刚性盒子中装有处于非平衡态的理想气体，那么经过足够时间后，系统的确会达到一个平衡态. 此时如果稍微增大盒子的体积，譬如说在一个大盒子中撤掉挡板，使得气体分子能到达的有效空间增加，那么系统就会开始向新的平衡态演化. 当系统达到新的平衡态时，内能不变，而熵却会增加！换句话来说，孤立演化过程中，内能守恒，但熵并不是一个守恒量. 看起来只有加上诸如局域平衡的条件，才能勉强对非平衡系统给出熵的定义.

当然，这是因为熵本身就与过程的不可逆性有关. 譬如说一旦两个不同温度的物体相互接触发生了自发的热传递，那么就不可能将热传递的痕迹完全消除. 这就是说，热传导过程是不可逆的. 这就是热力学第二定律的 Clausius 表述.

现在讨论热力学第一定律的微分形式. 假设平衡态体系由内能 以及其它广义坐标 所完全刻画，也即态空间构成一个 维流形 那么一般来说无穷小过程中的做功可以由 形式 来表示, 其中 为广义坐标 对应的广义力，或者是响应函数. 对于准静态过程来说，系统本身的相应性质(如压强)与外界的相应性质相同: 这是根据力学平衡得出的，也即是经典力学的推论.

自然，态函数 的无穷小增量可以表示为恰当微分 因此有 因而无穷小过程中的热量就被表示为了两个 1-形式之差：

一般来说功形式并不是恰当的，因而热量也不是恰当的.

以上关于热力学第一定律的微分形式的讨论都是局限于平衡态流形 上的过程，也即准静态过程说的. 之前已经提过，内能可以推广至非平衡体系，因此实际上对于任意的过程(包括不可逆和非平衡过程)，内能在整个过程中都可以看作是一个定义良好的态函数，因而 形式 仍然是有意义的. 不过此时系统自身的广义力(如压强)一般来说与外界的广义力不再相等，甚至可能是未定义的(如理想气体的自由膨胀过程)，因而功形式的系数由外部的广义力给出： . 因此可以得到热力学第一定律的微分形式的推广为 此时，由于功形式依赖于外部变量，因此热量 也依赖于外部变量，但二者之和则是纯粹的态变量. 也可以把此时的热力学流形进行扩张，将环境中的参量也加入进去，得到增广的流形 使得式 尽可能地接近 的形式.

热力学中经常需要作自变量的替换，也即将流形 的坐标 替换为另一组. 某个坐标变换 是否可行，关键是要检查变换的 Jacobi 矩阵的秩. 之后将会给出一些可行和不可行的变换的例子.

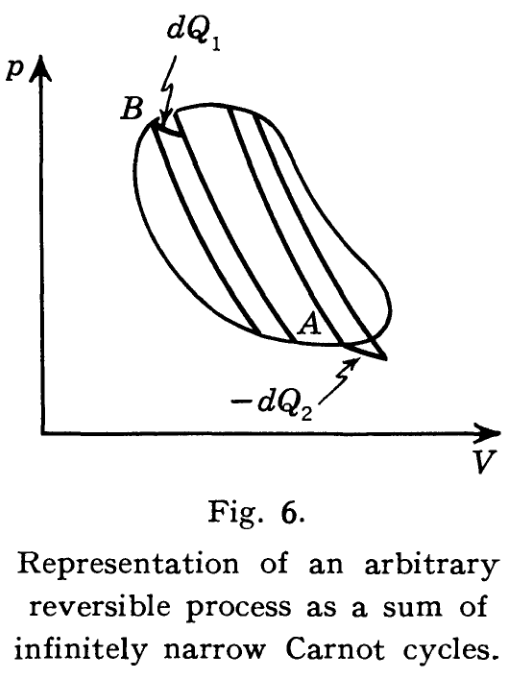
Carnot 定理

根据热力学第二定律的 Kelvin 表述可以导出 Carnot 定理(文献 [1], pp.78, 文献[2], pp.64)：

工作在高温热源 和低温热源 之间的可逆卡诺热机的效率与工质无关，只依赖于热源的温度 : 此外，任何不可逆的 Carnot 热机的效率都小于可逆 Carnot 热机的效率: 等式 的证明是经典的：假设两个 Carnot 热机具有不同的效率，那么可利用效率较大者做的功反向驱动效率较小者，二者联合工作的总的效果就是从热源 吸收热量并全部转化为功，从而违反 Kelvin 表述. 这就表明了工作在两个温度不同热源之间的 Carnot 热机的效率必定相同，也即 Carnot 热机的效率仅是热源温度 的函数.

至于不等式 的证明，则需要利用对可逆过程的定义. 文献 [2] (pp. 61)将可逆过程定义得比准静态过程更加宽泛：对于任意一个过程 如果存在另一个过程 使得系统及其环境同时恢复原状，那么就称过程 为一个可逆过程. 在这个定义中，并不要求逆过程的每一步都是原过程的反演. 因而这种定义会使得可逆过程的范畴大为增加，同时也使得不可逆过程的范围缩小. 特别地，按照这个定义，可逆过程未必是准静态的，因此即便是可逆 Carnot 热机，其与热源接触时也可能不是一直保持等温的.

有了这个定义，就很容易证明不可逆 Carnot 热机的效率小于可逆 Carnot 热机的效率了：对于一个不可逆的 Carnot 热机，利用与等式 本质上相同的论证可以证明其效率不大于可逆 Carnot 热机的效率. 另一方面，若不可逆 Carnot 热机的效率等于可逆 Carnot 热机的效率，那么如果用该不可逆 Carnot 热机输出的功来反向驱动一台工作于相同热源下的 Carnot 热机，那么二者联合工作的总的效果就是使得热机以及热源的状态都恢复原状，这就表明该不可逆 Carnot 热机实际上是可逆的，从而导致矛盾！

看起来放宽可逆性的定义是严格不等式 的一个比较好的导出办法，如果坚持要求可逆过程是准静态的，那么恐怕就必须将严格不等式 作为一条经验事实来接受了.

由 Carnot 定理以及热机效率的定义可以导出一个新的温标，也即热力学温标： 注意，式 中严格来说只是对热源定义了热力学温标，不过利用热平衡定律可以将其引申至任意平衡态体系.

这个时候，就可以注意到等式

Clausius 不等式

接下来就是 Clausius 不等式的证明： 假设一个系统经历了一个循环过程，在该过程中依次与温度为 的热源接触，从第 个热源吸收的热量记为 那么有以下不等式成立：

其中不等号严格成立当且仅当该过程为不可逆过程.

不等式 的证明并不困难，主要还是依赖于引入假想的 Carnot 循环：假设有一个高温热源 其温度高于所有的 热源，并构造 个 Carnot 热机，使得每个热机工作在热源 和 之间，并且令第 个 Carnot 热机向热源 放出的热量恰好等于 那么其从热源 吸收的热量为 这 个 Carnot 热机联合工作的效果就是将 个热源全部恢复原状，以及从热源 提取了热量 如果再加上系统原本的循环，那么这整个大过程的效果就是，系统和 个热源均恢复原状，从热源 吸热 外界做的总功为对系统做功 与对 Carnot 热机做功 之和，也即 对外做功的量为 根据热力学第二定律的 Kelvin 表述，这个值不可能大于零，因此就得到 Clausius 不等式 (11).

Clausius 不等式的以上证明思路可见于文献 [1] pp.120, 文献 [2] pp.70 以及文献 [3] pp.46.

当不等式 中的等号成立时，假想的 Carnot 循环实际上就是在 个热源之间合理地分配热量，使得每个热源都恢复原状，并且最终从大热源 的吸热也为零. 换句话说，系统的环境完全恢复原状. 这就表明体系所经历的原始循环是可逆的. 当然，这也表明原始的循环只涉及到熵流，而没有熵产.

反之，假设不等式 中的不等号严格成立，那么假想的 Carnot 循环与原循环的总的效应就是，外界对整个大系统做功并完全转化为热. 毫无疑问，这种耗散过程是不可逆的(见文献 [1] pp.74 的讨论). 另一方面，考虑到可逆过程与可逆过程的联合过程必定也是可逆的，因此如果原始循环本身可逆，那么其与 Carnot 循环联合构成的大循环也应当是可逆的. 由此即可断定原始循环本身是不可逆的.

总之，以上讨论证明了 Clausius 不等式 (11) 中的不等号当且仅当循环不可逆时才是严格的.

还有一些值得推敲的细节就是，在 Clausius 不等式的叙述中，似乎默认 个热源是彼此不同的，系统只是依次与这些热源发生接触. 既然这些热源是独立的，因此 Carnot 热机可以单独地与这每一个热源接触而运作起来. 倘若假设某个热源并非是一个大热库，而是有限体系，那么系统与热源的接触就有可能使得热源的温度发生变化. 不妨假设温度的变化是离散的，譬如说系统与某个小热源接触，使得小热源的温度依次从 变为 不同温度的切换过程可以忽略，那么先前的 Carnot 热机的论证是否还能应用？毕竟现在热源只有一个，不同的温度只是同一个热源在不同时间下的状态. 这个时候是不是需要在不同的时刻都部署一台 Carnot 热机？

其实，只要假设系统与热库的相互作用只涉及到传热，那么 Carnot 热机的思想实验就仍然适用. 毕竟此时导致热源温度变化的原因无非就是与系统之间的传热，因此不妨等到原始循环结束之后，再把热源接上 Carnot 热机进行操作，那么热量 的反向传递理应会使得热源的温度从 回复到 由此类推最终可恢复到原状. 因而热源的同一性也并不构成本质障碍.

另一个值得注意的地方就是，在系统与不同的热源接触的空挡，是不是默认系统一定是绝热的？至少对于 Carnot 循环来说，当系统不与热源接触时，系统一定是绝热的. 或者说，一般来说默认系统总是从热源吸热或放热，因此如果系统不与任何热源接触，传热就无从谈起. 这个细节对于有限多个热源来说并没有那么碍事，但是对于温度连续变化的情况来说，就有些惹眼了.

为了同时考虑平衡和非平衡过程，以下假设系统的状态空间为增广的状态流形 假设系统经历一个连续的循环过程 其环境的温度为连续变量 那么就可以考虑如下环路积分 通常要证明该积分小于等于零，一个思路就是利用 Carnot 循环来逼近回路 但是回路 的形状可以是任意的，因此要证明 Carnot 循环的逼近可达到任意精度并不容易. 下图是文献 [4] pp.31 对此思路的一个示意图(当然，也仅仅是一个示意图！).

在接下来导出连续形式的 Clausius 不等式之前，首先需要证明一个关于热源温度可变的 Carnot 热机的引理：

引理 1：设热机工作在两个热源 之间，其中热源 的温度 固定，并且总是大于热源 的温度 若热机与热源 接触时，热源 的温度可变，那么热机的效率 满足不等式 事实上，若 那么就可以用该热机输出的功反向驱动一个工作在热源 和温度为 的热源 之间的 Carnot 热机，使得两台热机联合运行的总效果为从低温热源 和 传热给了高温热源 从而违背热力学第二定律的 Clausius 表述. 同理可证明

下面利用离散形式的 Clausius 不等式来推出其连续形式. 这里仍然需要之前提出的一个假设，那就是系统与环境之间的相互作用只涉及到传热，也就是说系统对外做功并不是直接对环境做功. 换言之，系统的与外界的相互作用可分为两部分:其一是"热环境"，其二则是"力学环境". 一个例子就是封闭在气缸中的气体，缸体本身是透热的，因而气体可以从气缸外部的热源吸收热量；另一方面假设气缸内的活塞是隔热的，因而气体膨胀或收缩时，对活塞所连接的外部机构仅仅是做了功，而没有发生传热. 这就是把系统的总的环境分为了热源和功源两个独立的部分.

其次就是需要假设，当热环境的温度从 变为 时，其所需要的传热 会随着 趋于零而趋于零.

接下来就可以开始论证了. 将区间 划分为 个等长的小区间 并且记在区间 上系统从热环境吸收的热量为 也即

现在在循环 结束之后，考虑一个假想的离散过程，在其中我们引入一个高温热源 其温度高于 在 上的任意取值，并构造 个 Carnot 热机，其中第 个热机工作在热源 和循环 刚结束时温度为 的热环境之间，令该 Carnot 热机向热环境放出的热量恰好等于 那么根据引理 1 可知，其从高温热源 吸收的热量 满足 其中 表示函数 在区间 上的振幅. 第一个 Carnot 循环结束后，热源温度变为 现在引入第二个 Carnot 热机，使得其向热环境放出的热量恰好等于 那么其从高温热源 吸收的热量 满足 如此迭代，那么经历 轮 Carnot 循环后，系统的热环境恢复原状，总的效果为从大热源吸热 并完全转化为功.根据先前的估计可得

根据热力学第二定律的 Kelvin 表述， 的值必定小于等于零，由此即得

现在令 那么区间 的长度趋于零，因而闭区间上的一致连续函数 的振幅也一致趋于零. 自然， 是有界的，因而不等式 右边趋于零. 至于 式的左边，容易验证 位于积分 在区间 的上和与下和之间，因而当 时，左边的求和收敛到 这就证明了 Clausius 不等式的连续形式：

下面考虑不等式中的不等号严格成立的条件. 当不等式 中的等号成立时，假想的 Carnot 循环实际上就是在 个热源之间合理地分配热量，使得每个热源都恢复原状，并且最终从大热源 的总的吸热也为零. 换句话说，系统的环境完全恢复原状. 这就表明体系所经历的原始循环是可逆的.

反之，假设不等式 中的不等号严格成立，那么假想的 Carnot 循环与原循环的总的效应就是，外界对整个大系统做功并完全转化为热. 毫无疑问，这种耗散过程是不可逆的. 另一方面，考虑到可逆过程与可逆过程的联合过程必定也是可逆的，因此如果原始循环本身可逆，那么其与 Carnot 循环联合构成的大循环也应当是可逆的. 由此即可断定原始循环本身是不可逆的.

总之，现在我们就证明了 Clausius 不等式的连续形式.

熵

对于可逆过程来说， Clausius 不等式成为一个积分等式. 由于其对于态空间 上的任意闭合回路 都成立，因此对于任意的二维子流形 都有

现在令 收缩为一点，那么即可得到 在该点处的值为零. 这表明 形式 是闭的. 特别地，假设 是单连通的，那么 就是恰当的，因而存在函数 使得 该函数 称为熵. 自然， 的定义始终存在一个任意加性常数，不过该常数可以通过热力学第三定律加以确定.

式 表明 是热量形式 的一个积分因子. 根据 Frobenius 定理(文献 [5] pp.83), 可积的充分必要条件为 将热力学第一定律 (5) 式代入，那么可积条件 (26) 可以写为 使用 作为流形 上的一组坐标，那么就有 因此可积条件 可写为

由此即得对于 有

以及对于任意的互不相同的指标 均有

当然，式 和 式 分别只对 和 的情形成立. 当系统除内能外可以只由一个广义坐标描述时，譬如说给定质量的理想气体系统， 自动成立，因此这种系统的热量形式自动是可积的，从而其熵函数 也自动存在.

对于参量较多的系统来说，式 和 式 是热力学第一和第二定律对系统的状态量的性质的一个基本规定. 任何实际的热力学系统都应当满足这些约束关系. Maxwell 关系实际上就是这些约束关系中的一小部分. 这些热力学恒等式并不是纯粹数学的，而是由热力学基本定律所导出的.

表象问题

此处又可引申出一个问题，也即热力学的多种不同的表象. 其实这无非是取态空间 的不同的坐标. 最基本的内能表象 是由热力学第一定律所规定的，而把内能 替换为熵 就得到了熵表象. 要证明熵表象的合理性，需要验证 是流形 的一组坐标. 为此，直接计算 Jacobi 矩阵

可知该矩阵的行列式为 由此即知 确是流形 的一组坐标. 因此熵表象是合理的.

接下来我们证明广义坐标 所对应的相应函数(或者说广义力) 与 之间存在某种对偶性: 如果把 替换为 那么就可以得到一组新的坐标. 譬如说以内能表象 为例. 将 替换为 那么不妨将内能调换为第二个坐标，那么就可以 Jacobi 矩阵

显然，该矩阵的行列式等于 因此表象 的合理性取决于 关于 的偏导数是否恒为零. 由于响应函数 的具体表达式因系统而异，因此似乎这个问题并没有一个确切的答案. 但对于实际的热力学系统来说，除了热力学恒等式 和 之外，仍然存在着一些其他的物理约束(见下文)，使得 因此，总是可以用相应函数来替换相应的广义坐标，以得到一组新的表象.

熵增加原理

现在讨论任意过程的熵变. 设平衡态 经过某个过程 达到平衡态 那么如果 为可逆过程，也即 上的一条路径，那么就有

另一方面，假设 为不可逆过程，那么令 为从 到 的一个可逆过程，那么 就构成一个不可逆循环，应用 Clausius 不等式即得

另一方面，由于 为可逆过程，因此应用 式即得

代入 式即得不可逆过程的熵变所满足的不等式

总之，对于任意过程 ，都有

成立，并且不等号严格成立当且仅当 为不可逆过程. 考虑到 代表系统与外界的热交换，因而对应着熵流，因此不可逆过程熵的额外增加实际上是对应于系统内部的熵产生. 不过其实熵流与熵产生的界定也并非总是那么分明，而是依赖于系统边界的选取：譬如说如果把高温物体与低温物体所组成的系统考虑为一个大系统，那么两个物体之间的自发传热就成为大系统的熵产，但是如果以单个物体为系统来看的话则是熵流.

当然，如果系统从一个平衡态经历绝热可逆过程到达另一平衡态，那么根据 式系统的熵保持不变. 也就是说绝热可逆过程是等熵的. 另一方面，对于不可逆的绝热过程来说，由 式可知熵变必定大于零. 这表明绝热过程满足以下不等式： 并且不等号严格成立当且仅当绝热过程是不可逆的.

以上的不等式 和 假定了系统的初末态为平衡态. 不过该不等式也可以推广至非平衡态(至少可以推广到局域平衡态). 对于局域平衡态来说，其熵定义为各个局域平衡态的熵之和. 在这个意义上，我们就得到了熵增加原理:孤立体系的熵永远不会减少:

这个原理对于判断系统自发变动的方向以及判断平衡的稳定性特别有用.

自发过程的方向判定

由熵变的不等式 可以得到系统在各种约束条件下，实际过程的发生的方向.

譬如说对于孤立系统来说，实际过程必定满足 一个常见的论断就是孤立系统在平衡态时必定达到熵的极大值(文献 [2], pp.76): 这里的极大值是关于孤立系统的所有可能的局域平衡态所组成的空间 说的. 如果系统的熵在 的某个态 处取得(局部)极大值，那么 任何附近的态都不会被达到：从 出发，任意假想的过程都会使得熵减小，从而违背熵增加原理. 不过其实反过来的论证并不一定为真：即便系统的熵不是局部极大值，但是只要存在一些额外的条件(譬如说非热力学的限制)来限制可能的变动，那么系统仍然可以保持平衡.

因此，更合适的说法是：在只考虑热力学第二定律的约束下，孤立系统的平衡态必定达到熵的极大值. 如果考虑无穷小过程，就可以得到孤立系统的实际过程的方向判定条件为 为了与微分记号相区别，这里使用 表示无穷小差分. 当不等式中取等号时，对应于可逆过程，而取不等号时则对应于不可逆过程，也即自发过程.

当然可以考虑系统的其他约束条件. 譬如说可以考虑等熵约束 那么实际过程所需满足的条件为 如果考虑无穷小过程，就可以得到等熵系统的实际过程的方向判定条件，也即 当不等式中取等号时，对应于可逆过程，而取不等号时则对应于不可逆过程，也即自发过程.

如果进一步考虑与外界没有功交换(作功)的系统，也即 那么实际过程所需满足的条件为 由此可知，对于与外界没有功交换的等熵系统，在只考虑热力学第二定律的约束下，其在平衡态时必定达到内能的极小值. 也即内能极小原理.

如果考虑无穷小过程，就可以得到与外界没有能量交换等熵系统的实际过程的方向判定条件，也即 当不等式中取等号时，对应于可逆过程，而取不等号时则对应于不可逆过程，也即自发过程.

接下来考虑两类有广泛实际应用的约束条件. 其一是考虑等温系统. 那么实际过程所需满足的条件为 或者说 也即 这里 为 Helmholtz 自由能. 如果考虑无穷小过程，就可以得到等温系统的实际过程的方向判定条件，也即 当不等式中取等号时，对应于可逆过程，而取不等号时则对应于不可逆过程，也即自发过程.

如果进一步考虑与外界无功交换的等温系统，譬如对理想气体来说，可以考虑等温等容(且气体质量一定)系统，那么实际过程的方向的判定条件为 当不等式中取等号时，对应于可逆过程，而取不等号时则对应于不可逆过程，也即自发过程. 由此可知，对于与外界无功交换的等温系统，在只考虑热力学第二定律的约束下，其在平衡态时必定达到 Helmholtz 自由能的极小值. 也即Helmholtz 自由能极小原理. 如果考虑无穷小过程，就可以得到与外界无功交换的等温系统的实际过程的方向判定条件，也即 当不等式中取等号时，对应于可逆过程，而取不等号时则对应于不可逆过程，也即自发过程.

其二是考虑等温等压系统. 这里的"等压"指的是响应函数 均保持不变. 那么实际过程所需满足的条件仍然可以写为 不过由于响应函数的值固定，因此此时功 可以写为 于是就有 也即

这里 为 Gibbs 自由能. 当不等式中取等号时，对应于可逆过程，而取不等号时则对应于不可逆过程，也即自发过程. 由此可知，对于等温等压系统，在只考虑热力学第二定律的约束下，其在平衡态时必定达到 Gibbs 自由能的极小值. 也即Gibbs 自由能极小原理. 如果考虑无穷小过程，就可以得到等温等压系统的实际过程的方向判定条件，也即 当不等式中取等号时，对应于可逆过程，而取不等号时则对应于不可逆过程，也即自发过程.

Helmholtz 自由能

Helmholtz 自由能的一个物理意义就是，考虑系统从 态(平衡态或局域平衡态)出发，经历任意等温可逆过程 到达 态，那么系统对外做的功为

当然，由于 为等温过程，因此 于是 另一方面，若 为等温不可逆过程，那么由熵变不等式 可得 于是就有 由此可见，系统在等温过程中所能对外做的最大功正是初态的与末态的 Helmholtz 自由能之差. 因此 Helmholtz 自由能 衡量了系统在等温条件下对外做功的最大能力.

自然，由不等式 可知，若系统经历一个等温无功过程(对理想气体来说，可以考虑等温等容过程)，那么系统的 Helmholtz 自由能不可能增加. 并且对于不可逆(自发)过程，Helmholtz 自由能必定减小. 这表明任何自发过程总是沿着使得系统的 Helmholtz 自由能减小的方向，实际过程总是在消耗系统对外做功的能力(无论系统有没有对外做功).

自发过程的方向性与力学平衡

由 形式的等式 可得在 坐标下，有

如果两个系统相互接触，其某个特性函数分别为 和 并且这两个系统的内能 和 以及广义坐标 和 满足约束

那么内能 的虚变动 以及广义坐标 的虚变动 所导致的熵变为 由此即知平衡时，温度和响应函数满足

类似地，当 时，可以根据自发判据 来判定自发过程的方向. 譬如说假设 那么 要求 也即热量从系统 (a) 流向系统 (b). 类似地可以知道，当 时， 要求 也即广义坐标的变动沿着 的方向. 这也可以理解为热平衡定律和力学平衡的结果. 关键是考虑为什么热力学第二定律与这些其他的热力学以及力学定律相容. 实际上内能和熵的可加性假设至关重要，这是隐含地加入了某种模型，而这个模型恰好也是热力学和力学所使用的.

因此，有必要仔细地审查物理学的各个部门所使用的基本的模型和方法论，譬如系统的可加性等等，看看如何抽象为最基本的元素，然后讨论这些元素之组合，以及这些不同组合之间是否相容.

系统与环境的平衡条件

仿照之前的讨论也可以得到系统与环境的平衡条件. 假设系统一直与一个固定的环境接触，环境的温度和响应函数为常量 那么实际过程的判断条件为

特别地，当系统一直与环境相接触时，实际的无穷小过程的判断条件为 当系统本身处于平衡态时，可以认为任何无穷小过程都被热力学第二定律所阻止，也就是说，状态空间 内任意的无穷小虚变动 都不满足判定条件 也即 将 式代入即得平衡条件 这与式 是类似的.

平衡条件与平衡的稳定性

先前导出的平衡条件，实际上都是假设了系统在平衡态附近，任意无穷小的虚变动都不可能发生. 如果假设系统从任意初态出发，演化足够长时间后所到达的终态(平衡态)是唯一的，与演化历程无关，那么以上假设就是合理的. 在这个假设中，实际上是认为系统达到平衡态后就不再经历任何宏观变化，因而状态空间的任意虚变动都是被禁止的. 这就是说系统的平衡是(局部)稳定的. 如果任意有限的变动都被热力学第二定律所禁止，那么就是说系统的平衡是全局稳定的：在给定约束条件下，任意初态经历足够长的时间后都会到达该平衡态. 譬如说考虑一个孤立系统，其所对应的状态空间 (这实际上是整个状态空间的一个子流形)，这里将局域平衡态也纳入考虑范围，如果 是 的全局平衡态，那么从该空间的任意一个状态出发，演化足够久之后都会到达唯一的全局平衡态

然而许多实际系统也存在所谓的亚稳态乃至于随遇稳态. 亚稳态是说，虽然无穷小的虚变动都是禁止的，但存在一些有限的可发生的变动(跳跃). 这往往与相变相联系. 随遇稳态则是说，系统满足平衡条件 但存在一些不被禁止的无穷小虚变动. 这就是说，在 的切空间中，存在一些方向，使得在这些方向上

前面也提到了诸如等熵约束、等温约束等约束条件. 在这些约束条件下，可以根据平衡的局部稳定性假设导出一些热力学不等式. 譬如说在等温等容条件下，环境温度固定为 系统的可用的状态空间 由 给出(实际上是 的积分流形)，那么由平衡的局部稳定性可导出，在系统的平衡态 处， 在 的切空间中的任意非零向量上的取值均小于零，于是就有 这只不过是平衡条件. 由 在给定平衡态 的一个小邻域内小于零可得知(严格来说，存在二阶和三阶导数为零，四阶导数正定的可能性，这里不考虑这种简并情况) 在该平衡态处的二阶导数大于零(定义域为 因而此时 是关于 的单变量函数)，也即 或者说 由此可得热力学不等式

类似地可以得到其他的热力学不等式. 一个最为通用的办法是，考虑等温等压约束，此时系统与温度为 响应函数为 的环境接触，系统的可用的状态空间为 由平衡的局部稳定性可导出，在系统的平衡态 的一个小邻域内， 总是小于零，于是有 并且(固定温度和响应函数条件下的) Gibbs 自由能 在 处的 Hessian 矩阵 为正定矩阵. 这意味着该矩阵的每一个主子式都大于零. 特别地，对角线上的每个元素都大于零. 作为一个例子，有 对于理想气体来说， 因此这意味着理想气体体积膨胀时，压强会减小. 现在可以看到这是平衡稳定性的一个要求. 通过检查这些热力学不等式的违背情况也可以提示相变的发生.

不等式 的另一个重要用途是指示了表象变换的可能性. 式表明，从平衡的稳定性可以导出 Jacobi 矩阵 非退化，因而可以将表象 中的广义坐标 替换为响应函数 得到新的表象 这也说明了为什么理想气体的状态参量既可以用 也可以用 利用其他的热力学不等式可以进一步得到表象 和